Tribonacci Constant Conjugate, $y=\frac{x-1}{x}$ and the Unit Circle

The tribonacci numbers are defined by the recurrence relation

$$ q_n = q_{n-1} + q_{n-2} + q_{n-3} $$

where the initial terms are $ q_0 = 0 $, $ q_1=0 $ and $ q_2=1 $ [1]. The first few tribonacci numbers are

$$ 0,0,1,1,2,4,7,13,24,44,81,149,274, 504, 927, 1705, 3136, 5768, \ldots $$

(sequence A000073 in the OEIS)

The name tribonacci was given by a fourteen-year old junior high student Mark Feinberg in his paper "Fibonacci-Tribonacci" published by Fibonacci Quarterly in 1963 [1].

"The series was first described formally by Agronomof in 1914" [Wikipedia] but an earlier documented case of its use can be traced to Charles Darwin in the Origin of Species to describe the hypothetical population growth of elephants [2]. The problem limited reproductive elephants to three consecutive generations.

Like the Fibonacci numbers, the tribonacci numbers are convergent. The ratio of consecutive terms $\frac{q_{n+1}}{q_n}$ converges to $1.83928675$, known as the tribonacci constant [1]. The reciprocal of the tribonacci constant is $0.54368901$.

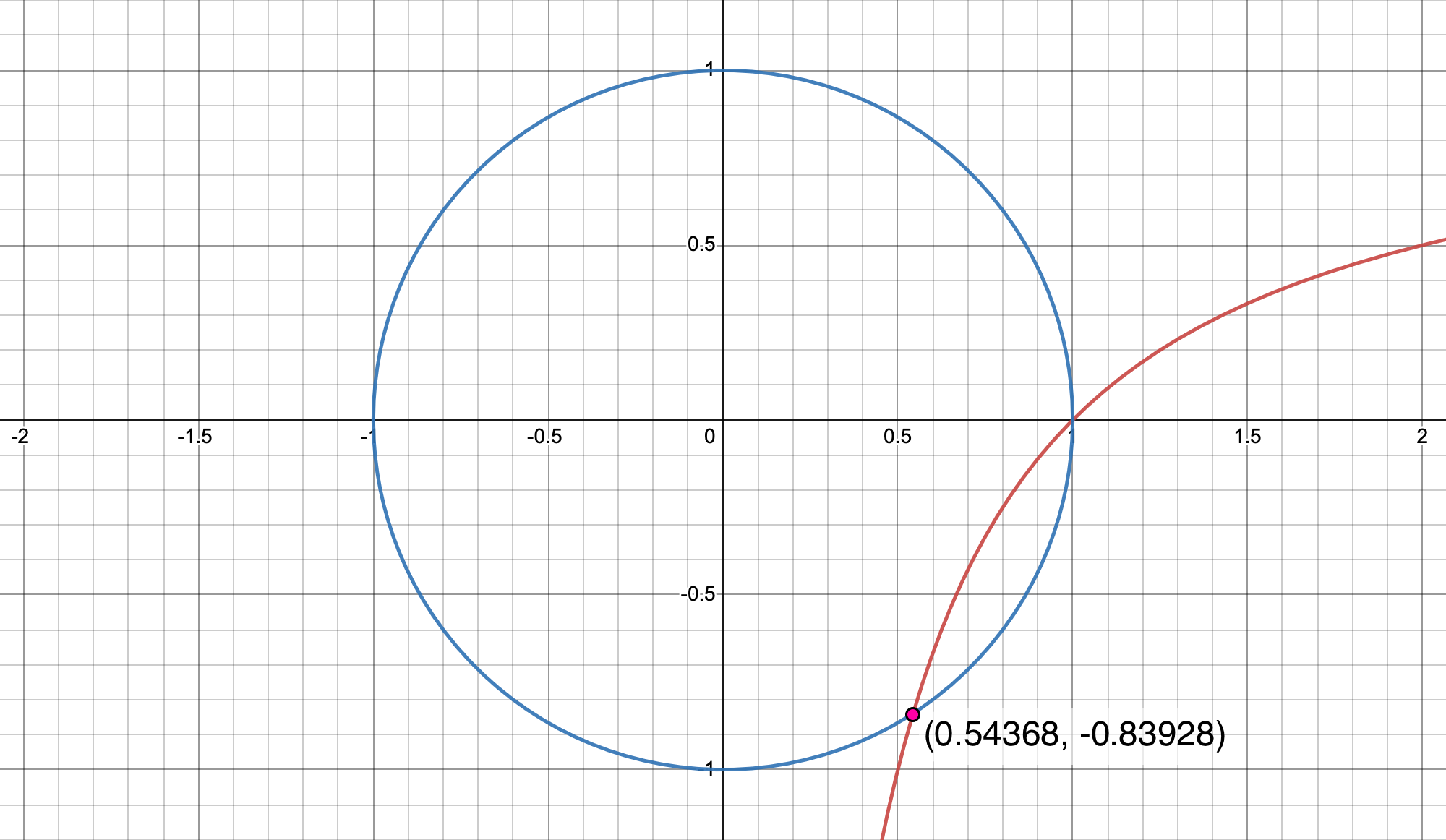
We first define the two equations that are to intersect. The first equation is

$$ y = \frac{x-1}{x} \tag{1} $$

and the second equation is for the unit circle

$$ x^2 + y^2 = 1 \text. \tag{2} $$

To find the intersections between $y = \frac{x-1}{x}$ and the unit circle we substitute equation (1) into equation (2):

$$ x^2 + \left(\frac{x-1}{x}\right)^2 = 1 $$

and simplified is $x^4 - 2x + 1 = 0$. Solving for $x$ we have

$$ \begin{aligned} x_1 &= 1 \\[2em] x_2 &= \frac{1}{3} \left( -1 - \frac{2}{\sqrt[3]{17+3\sqrt{33}}} + \sqrt[3]{17+3\sqrt{33}} \right) \\[1em] &\approx 0.54368901 \\[2em] x_3 &= \frac{1}{6} \left( -2 + \frac{2-2i\sqrt{3}}{\sqrt[3]{17+3\sqrt{33}}} + (-1-i\sqrt{3}) \sqrt[3]{17+3\sqrt{33}} \right) \\[2em] x_4 &= \frac{1}{6} \left( -2 + \frac{2+2i\sqrt{3}}{\sqrt[3]{17+3\sqrt{33}}} + i(\sqrt{3} + i) \sqrt[3]{17+3\sqrt{33}} \right) \text. \end{aligned} $$

WolframAlpha

The real intersection points are $(1, 0)$ and $(0.543689, -0.839286)$.

To check our answer we substitute $(0.543689, -0.839286)$ into equation (2) and we have

$$ (0.543689)^2 + (0.839286)^2 = 1 \text. $$

Source: Wikipedia

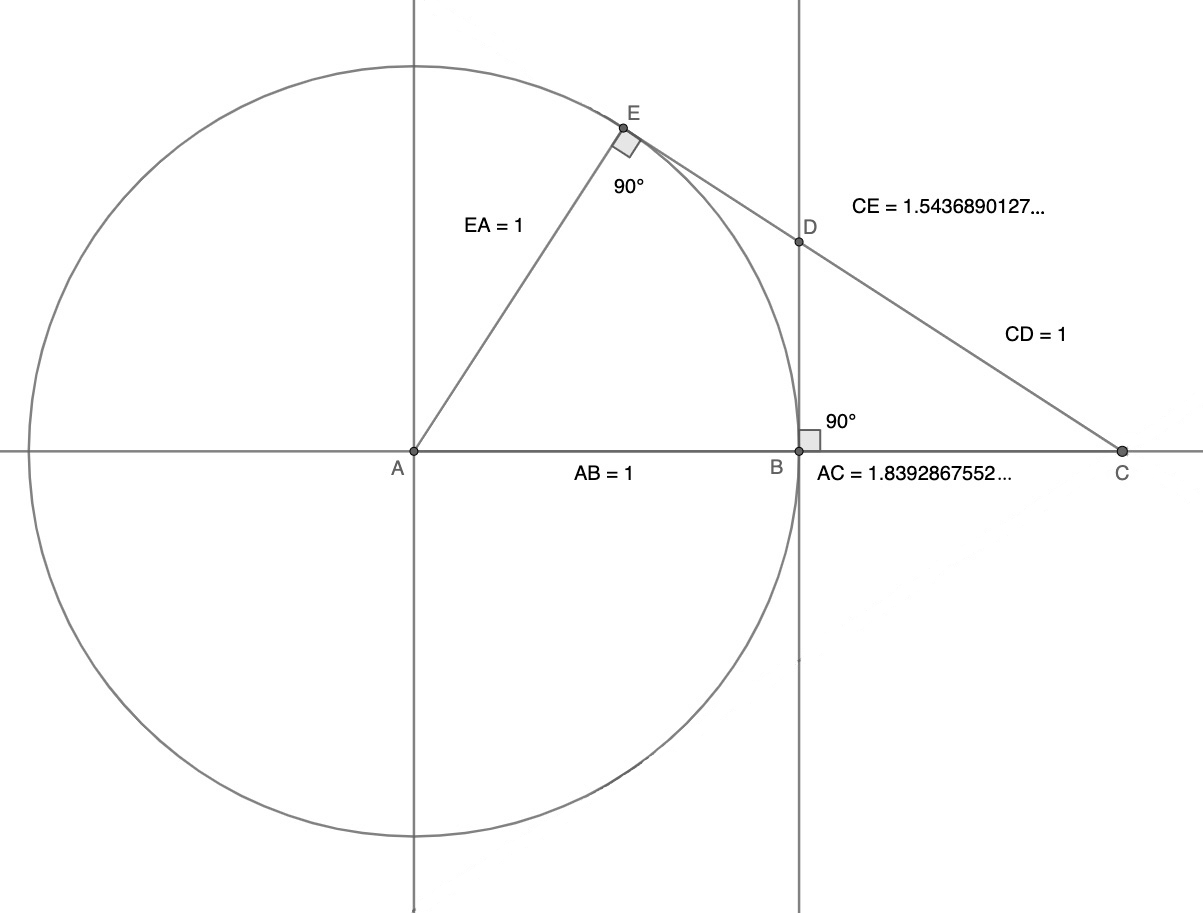
A geometric construction of the tribonacci constant with marked ruler and compass

by Xerardo Neira

Download paper

---

We first draw a unit circle with origin at $A$, and then a straight line, the vertical tangent passing through $B$: now, we must put the marked ruler against the circle as another tangent, while putting the marks for the length of the radius on the $AB$ line and the tangent passing through $B$, creating point $C$, point $D$ and point $E$. Now, let's call segment $AC$ as $t$: so, we can see two equations for the angle $BCD$, $\sin(BCD) = \frac{1}{t}$ and $\cos(BCD) = \frac{1 - t}{1}$ , and, from $\sin^2 + \cos^2 = 1$ , that leads to a quartic equation, $t^4 - 2t^3 + 1 = 0$ , which has the next factorization: $$ (t-1)(t^3-t^2-t-1) = 0 $$ This equation has two solutions: the first one, for $( t - 1 )$ , it will be evidently $t = 1$ , that is, the tangent on the unit circle; and the other one, for $( t^3 - t^2 - t - 1 )$ , as we established at the beginning of this article, has only one real solution, that is, the tribonacci constant. Quod erat demonstrandum.

1. Mark Feinberg, Fibonacci-Tetranacci, The Fibonacci Quarterly, 1.3, 71-74 (1963).
2. Podani, János; Kun, Ádám; Szilágyi, András, "How Fast Does Darwin's Elephant Population Grow?" (PDF). Journal of the History of Biology, 51.2, 259-281 (2018). doi:10.1007/s10739-017-9488-5

1. The Tremendous Tribonacci constant (tpiezas.wordpress.com)