Tribonacci Constant Conjugate, y=(x-1)/x & Unit Circle

0.54368901

is the tribonacci constant conjugate.

The tribonacci constant conjugate makes an appearance at the intersection of

y = \frac{x - 1}{x}

and a unit circle.

Table of contents

Introduction
Proof
Geometric construction
by Xerardo Niera
References
Links

Introduction

The tribonacci numbers are defined by the recurrence relation

q_{n} = q_{n - 1} + q_{n - 2} + q_{n - 3}

where the initial terms are $q_{0} = 0$ , $q_{1} = 0$ and $q_{2} = 1$ [1]. The first few tribonacci numbers are

0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, \dots

(sequence A000073 in the OEIS)

The name tribonacci was given by a fourteen-year old junior high student Mark Feinberg in his paper "Fibonacci-Tribonacci" published by Fibonacci Quarterly in 1963 [1].

"The series was first described formally by Agronomof in 1914" [Wikipedia] but an earlier documented case of its use can be traced to Charles Darwin in the Origin of Species to describe the hypothetical population growth of elephants [2]. The problem limited reproductive elephants to three consecutive generations.

Like the Fibonacci numbers, the tribonacci numbers are convergent. The ratio of consecutive terms $\frac{q_{n + 1}}{q_{n}}$ converges to $1.83928675$ , known as the tribonacci constant [1]. The reciprocal of the tribonacci constant is $0.54368901$ .

Proof

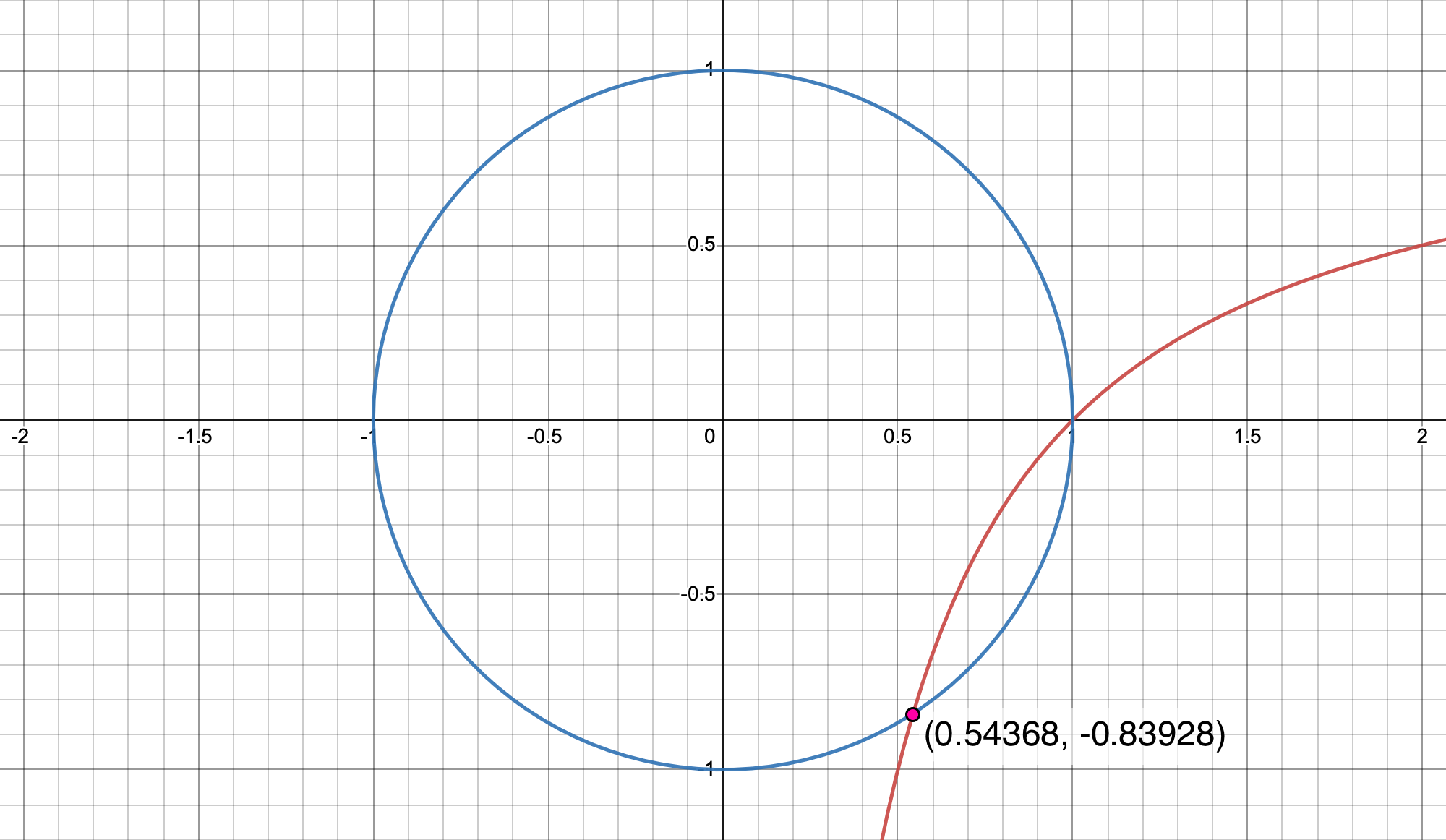
We first define the two equations that are to intersect. The first equation is

\begin{matrix} (1) & y = \frac{x - 1}{x} \end{matrix}

and the second equation is for the unit circle

\begin{matrix} (2) & x^{2} + y^{2} = 1 . \end{matrix}

To find the intersections between $y = \frac{x - 1}{x}$ and the unit circle we substitute equation (1) into equation (2):

x^{2} + {(\frac{x - 1}{x})}^{2} = 1

and simplified is $x^{4} - 2 x + 1 = 0$ . Solving for $x$ we have

\begin{aligned} x_{1} & = 1 \\ x_{2} & = \frac{1}{3} (- 1 - \frac{2}{\sqrt[3]{17 + 3 \sqrt{33}}} + \sqrt[3]{17 + 3 \sqrt{33}}) \\ \approx 0.54368901 \\ x_{3} & = \frac{1}{6} (- 2 + \frac{2 - 2 i \sqrt{3}}{\sqrt[3]{17 + 3 \sqrt{33}}} + (- 1 - i \sqrt{3}) \sqrt[3]{17 + 3 \sqrt{33}}) \\ x_{4} & = \frac{1}{6} (- 2 + \frac{2 + 2 i \sqrt{3}}{\sqrt[3]{17 + 3 \sqrt{33}}} + i (\sqrt{3} + i) \sqrt[3]{17 + 3 \sqrt{33}}) . \end{aligned}

WolframAlpha

The real intersection points are $(1, 0)$ and $(0.543689, - 0.839286)$ .

To check our answer we substitute $(0.543689, - 0.839286)$ into equation (2) and we have

(0.543689)^{2} + (0.839286)^{2} = 1 .

Geometric construction

Source: Wikipedia

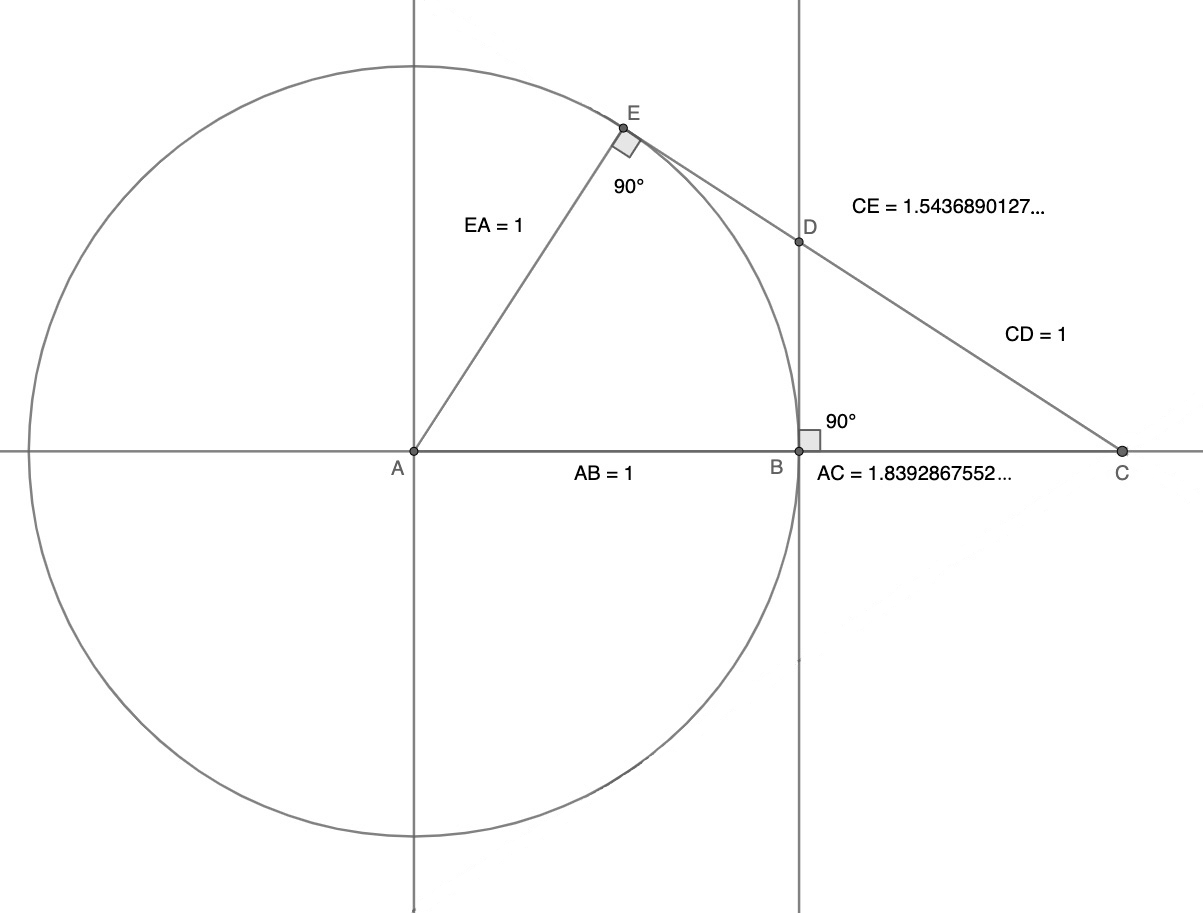
A geometric construction of the tribonacci constant with marked ruler and compass
by Xerardo Neira
Download paper

We first draw a unit circle with origin at $A$ , and then a straight line, the vertical tangent passing through $B$ : now, we must put the marked ruler against the circle as another tangent, while putting the marks for the length of the radius on the $A B$ line and the tangent passing through $B$ , creating point $C$ , point $D$ and point $E$ . Now, let's call segment $A C$ as $t$ : so, we can see two equations for the angle $B C D$ , $\sin (B C D) = \frac{1}{t}$ and $\cos (B C D) = \frac{1 - t}{1}$ , and, from $\sin^{2} + \cos^{2} = 1$ , that leads to a quartic equation, $t^{4} - 2 t^{3} + 1 = 0$ , which has the next factorization:
$(t - 1) (t^{3} - t^{2} - t - 1) = 0$
This equation has two solutions: the first one, for $(t - 1)$ , it will be evidently $t = 1$ , that is, the tangent on the unit circle; and the other one, for $(t^{3} - t^{2} - t - 1)$ , as we established at the beginning of this article, has only one real solution, that is, the tribonacci constant. Quod erat demonstrandum.

References

Mark Feinberg, Fibonacci-Tetranacci, The Fibonacci Quarterly, 1.3, 71-74 (1963).
Podani, János; Kun, Ádám; Szilágyi, András, "How Fast Does Darwin's Elephant Population Grow?" (PDF). Journal of the History of Biology, 51.2, 259-281 (2018). doi:10.1007/s10739-017-9488-5

Introduction

Proof

Geometric construction

A geometric construction of the tribonacci constant with marked ruler and compass

References

Links