Golden Ratio Conjugate, $y=x^2$ and the Unit Circle

The golden ratio is an irrational number also known as the golden mean, divine proportion, golden or divine section and belongs to the family of metallic means. The first definition of the golden ratio is given by Euclid in Elements and says the following:

Ακρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν.

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.

So how do we derive the golden ratio? We begin by translating Euclid's definition to $\frac{a}{b} = \frac{a+b}{a}$ and by substituting $a := x$ and $b := 1$ then simplifying, we have $x^2-x-1=0$. Solving for $x$ we have $x = \left\{ \frac{1+\sqrt{5}}{2}, \frac{1-\sqrt{5}}{2} \right\}$ or $x = \{1.618033988749, -0.618033988749 \}$. The positive root $\frac{1+\sqrt{5}}{2}$ or $1.618033988749$ is the golden ratio and is commonly denoted by phi ($\varphi$). The golden ratio conjugate is $\varphi^{-1} = \frac{\sqrt{5}-1}{2} = 0.618033988749$ and we will denote it with $\Phi$.

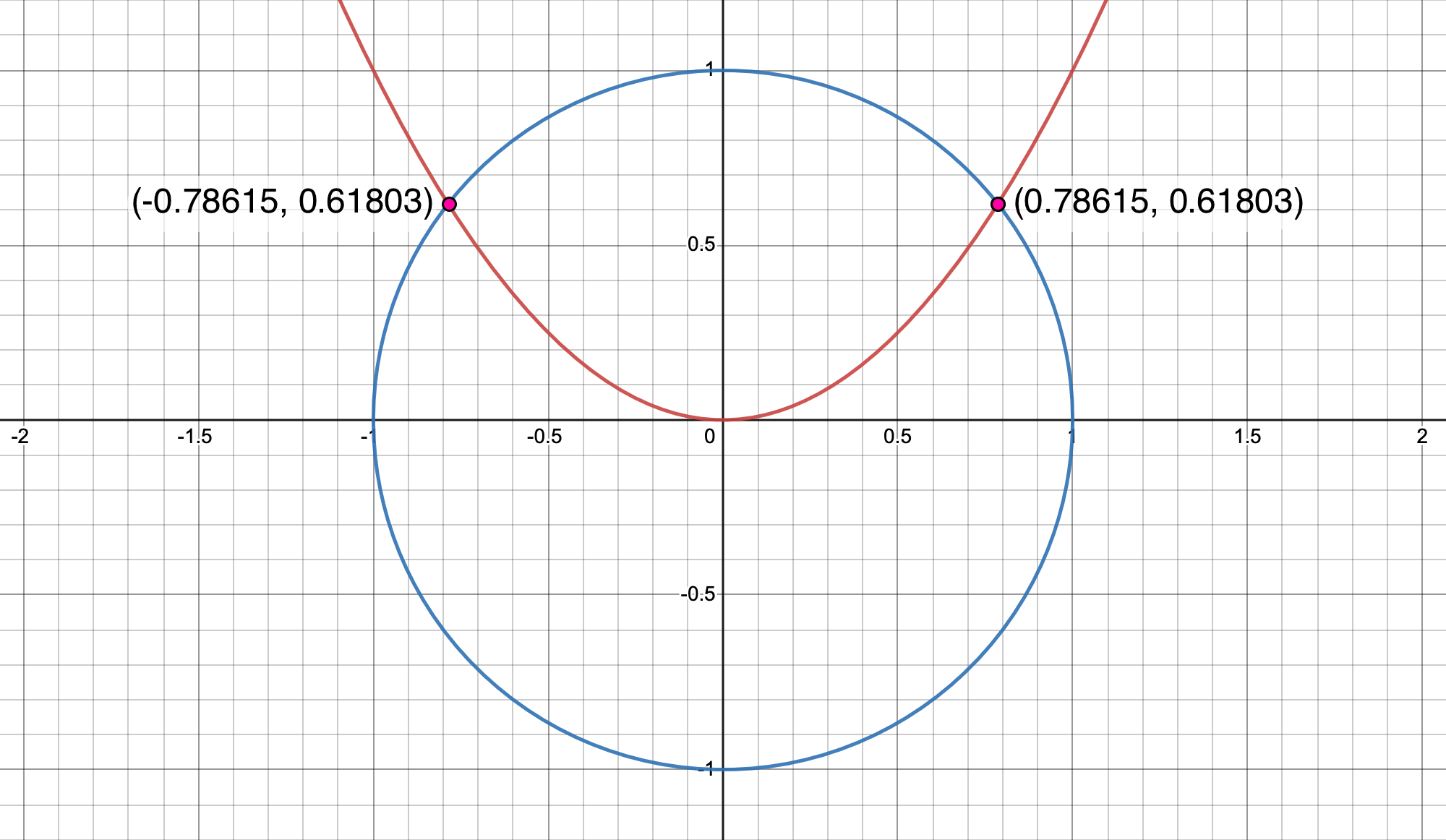
The equation for a basic parabola is $y = x^2$ and the equation for a unit circle is $x^2 + y^2 = 1 \text.$ To find the intersections we substitute $y=x^2$ into $x^2+y^2=1$ and we get $x^2 + x^4 = 1$. Solving for $x$ we have $x = \left\{ \pm \sqrt{\frac{\sqrt{5}-1}{2}},\ \pm i\sqrt{\frac{\sqrt{5}+1}{2}} \right\}$ or $x = \left\{ \pm \sqrt{\Phi},\ \pm i \sqrt{\varphi} \right\} \text.$

Solve $x^4+x^2-1=0$ with WolframAlpha

The real intersection points are $(\sqrt{\Phi}, \Phi)$ and $(-\sqrt{\Phi}, \Phi)$ and to check our answer we substitute $(\sqrt{\Phi},\Phi)$ into the equation for a unit circle and we have $(\sqrt{\Phi})^2 + \Phi^2 = 1 \text.$

1. Weisstein, Eric W. "Golden Ratio Conjugate." From MathWorld--A Wolfram Web Resource.